Алгоритмы сортировки

Сортировка выбором

Источники

Khan Academy - Selection sort

Сортировка вставками

Источники

Khan Academy - Insertion sort

Сортировка слиянием

Источники

Khan Academy - Merge sort

Быстрая сортировка

Дополнительная информация:

Общее представление

Так же как и сортировка слиянием, быстрая сортировка использует метод “разделяй и властвуй”, поэтому это рекурсивный алгоритм. Метод “разделяй и властвуй” в быстрой сортировке применяется несколько иначе, чем в сортировке слиянием. В сортировке слиянием на этапе разделения не выполняется почти никаких действий, и вся основная работа происходит на этапе соединения. Напротив, в быстрой сортировке вся основная работа выполняется на этапе разделения. Фактически на этапе соединения в быстрой сортировке ничего не происходит.

У быстрой сортировки есть и другие отличия от сортировки слиянием. Быстрая сортировка тут же сортирует массив. И время ее выполнения в худшем случае имеет такую же асимптотику, как и сортировка выбором и сортировка вставками: $\Theta(n^2)$. Но ее время выполнения в среднем асимптотически эквивалентно времени выполнения сортировки слиянием: $\Theta(n\log_2 n)$. Итак, почему стоит рассмотреть быструю сортировку, если сортировка слиянием по крайней мере не хуже? Дело в том, что постоянный множитель, спрятанный в обозначении $\Theta$, имеет достаточно неплохое значение у быстрой сортировки. На практике быстрая сортировка превосходит сортировку слиянием и существенно превосходит сортировку выбором и сортировку вставками.

Рассмотрим, как быстрая сортировка использует метод “разделяй и властвуй”. Как и в случае сортировки слиянием, рассмотрим задачу сортировки подмассива array[p..r], а изначальный подмассив – это array[0..n-1].

Разделение. Выберем любой элемент в подмассиве array[p..r]. Назовем этот элемент опорным. Переставим элементы в подмассиве array[p..r] таким образом, чтобы все элементы в array[p..r], которые меньше либо равны опорному элементу, находились слева от него, а все элементы, которые больше опорного элемента, находились справа от него. Эту процедуру мы будем называть разбиением. На этом этапе нам неважно, в каком порядке идут элементы, находящиеся слева от опорного элемента, и в каком порядке идут элементы, находящиеся справа от него. Нам важно только то, что каждый элемент находится с нужной стороны от опорного элемента.
На практике мы будем всегда выбирать в качестве опорного элемента самый правый элемент подмассива – array[r]. Например, если подмассив – [9, 7, 5, 11, 12, 2, 14, 3, 10, 6], то опорным элементом будет 6. После разбиения подмассив может выглядеть следующим образом: [5, 2, 3, 6, 12, 7, 14, 9, 10, 11]. Пусть q – индекс опорного элемента.
Властвование. Рекурсивно отсортируем подмассивы array[p..q-1] (все элементы слева от опорного элемента, которые должны быть меньше либо равны опорному элементу) и array[q+1..r] (все элементы справа от опорного элемента, которые должны быть больше опорного элемента).
Соединение. Ничего не нужно делать. После рекурсивных вызовов подмассив отсортирован. Почему? Все элементы слева от опорного элемента, array[p..q-1], меньше либо равны опорному элементу и отсортированы (согласно предположению индукции), а все элементы справа от опорного элемента, array[q+1..r], больше, чем опорный элемент, и тоже отсортированы. Поэтому элементы всего подмассива array[p..r] просто не могут быть не отсортированы!

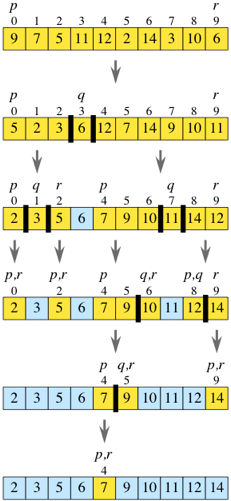
Рассмотрим наш пример. После рекурсивного вызова сортировки подмассивов слева и справа от опорного элемента подмассив слева от опорного элемента будет [2, 3, 5], подмассив справа от опорного элемента будет [7, 9, 10, 11, 12, 14]. Поэтому весь подмассив – это [2, 3, 5], за которым идет опорный элемент 6, после чего идут [7, 9, 10, 11, 12, 14]. Подмассив отсортирован.

Базовые случаи – это когда в подмассивах меньше двух элементов, как это было в сортировке слиянием. В сортировке слиянием у нас никогда не было подмассива без элементов, но такая ситуация возможна в быстрой сортировке, если все остальные элементы подмассива меньше опорного элемента или все они больше опорного элемента.

Вернемся к этапу властвования и разберем рекурсивную сортировку подмассивов. После первого разбиения у нас есть подмассивы [5, 2, 3] и [12, 7, 14, 9, 10, 11], а 6 – опорный элемент.

Чтобы отсортировать подмассив [5, 2, 3], мы выберем 3 в качестве опорного элемента. После разбиения получим [2, 3, 5]. Подмассив [2] слева от опорного элемента относится к базовому случаю при очередном рекурсивном вызове, как и подмассив [5] справа от опорного элемента.

Чтобы отсортировать подмассив [12, 7, 14, 9, 10, 11], выберем 11 в качестве опорного элемента, тогда получим [7, 9, 10] слева от опорного элемента и [14, 12] справа от него. После того, как эти подмассивы будут отсортированы, мы получим [7, 9, 10], дальше 11 и [12, 14].

На рисунке показана работа всего алгоритма быстрой сортировки. Элементы массива, выделенные голубым цветом, были опорными элементами на предшествующих рекурсивных вызовах, и поэтому эти элементы в дальнейшем не рассматриваются и не перемещаются.

Рис. 1

Разбиение за линейное время

Основная работа быстрой сортировки происходит на этапе разделения, который разбивает подмассив array[p..r] относительно опорного элемента, выбранного из этого подмассива. Хотя мы можем выбрать любой элемент подмассива в качестве опорного, легко реализовать разбиение, если выбрать опорным самый правый элемент подмассива – A[r].

После выбора опорного элемента алгоритм разбивает подмассив, проходя по нему слева направо и сравнивая каждый элемент с опорным. Хранятся два индекса q и j элементов подмассива, которые разделяют его на 4 группы. Мы используем имя переменной q, потому что этот индекс в конце концов укажет на наш опорный элемент. Мы используем имя j, потому что это имя часто используется для счетчика, и после выполнения процедуры разбиения эта переменная нам будет не нужна.

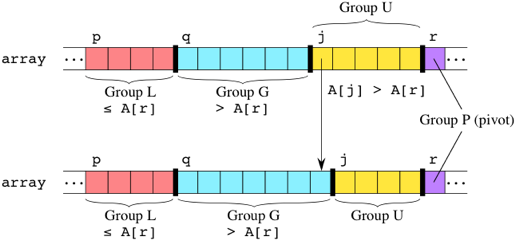
Элементы подмассива array[p..q-1] – это “группа L”, которая состоит из элементов, про которых известно, что они меньше (less) либо равны опорному элементу.
Элементы подмассива array[q..j-1] – это “группа G”, которая состоит из элементов, про которых известно, что они больше (greater), чем опорный элемент.
Элементы подмассива array[j..r-1] – это “группа U”, которая состоит из элементов, про которых неизвестно (unknown), как они соотносятся с опорным элементом, потому что они с ним еще не сравнивались.
Наконец, array[r] – это “группа P” – опорный элемент (pivot).

Сначала оба индекса q и j равны p. На каждом шаге мы сравниваем A[j], самый левый элемент в группе U, с опорным элементом. Если A[j] больше опорного элемента, то мы просто увеличиваем j на 1, и тогда линия между группами G и U сдвинется на один элемент вправо:

Рис. 2

Если же A[j] меньше либо равно опорному элементу, то мы меняем местами A[j] с A[q] (самым левым элементом в группе G), увеличиваем j на 1, тем самым линия между группами L и G, как и линия между группами G и U, сдвигается на один элемент вправо:

Рис. 3

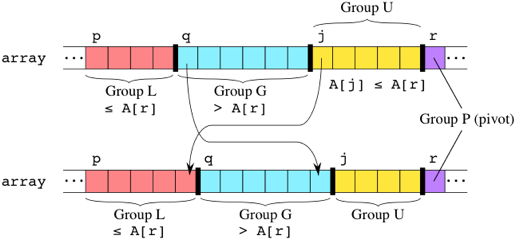
Когда мы дойдем до опорного элемента, группа U будет пустой. Остается поменять местами опорный элемент с самым левым элементом группы G: поменять местами A[r] и A[q]. Этот обмен помещает опорный элемент между группами L и G, и это правильный шаг, даже если группа L или группа G является пустой. (Если группа L пуста, то это значит, что q ни разу не увеличивалось и оставалось равным начальному значению p, поэтому опорный элемент становится на самое левое место в подмассиве. Если группа G пуста, то это означает, что q увеличивалось на единицу каждый раз, когда j увеличивалось на единицу, и поэтому, когда j достигло индекса опорного элемента r, то q = r, и обмен местами A[r] и A[q] оставляет опорный элемент на самом правом месте в подмассиве.) Функция partition, которая реализует эту идею, также возвращает индекс q, на котором оказался опорный элемент, поэтому функция quicksort, которая вызывает эту функцию, будет знать, где находится линия раздела между двумя частями подмассива. На рисунке показаны шаги разбиения подмассива [12, 7, 14, 9, 10, 11], который содержится в array[4..9]:

Рис. 4

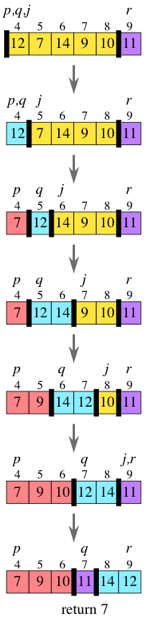
Разбиение подмассива из $n$ элементов займет $\Theta(n)$ времени. Каждый элемент A[j] сравнивается с опорным элементом ровно один раз. A[j] может обмениваться или не обмениваться местами с A[q], q может увеличиваться на 1 или не увеличиваться на 1, и j всегда увеличивается на 1. Общее число действий, выполненных для каждого элемента подмассива, – величина постоянная. Так как в подмассиве $n$ элементов, то время разбиения есть $\Theta(n)$: разбиение производится за линейное время.

Анализ быстрой сортировки

Как получается, что время выполнения быстрой сортировки оказывается различным в худшем и среднем случае? Начнем с рассмотрения времени выполнения в худшем случае. Предположим, что нам не повезло, и размеры частей разбиения сильно несбалансированны. В частности, предположим, что опорный элемент, выбранный функцией partition, – это всегда либо наименьший, либо наибольший элемент в $n$-элементном подмассиве. Тогда одна из частей разбиения не будет содержать элементов, а в другой будет $n-1$ элементов – все элементы, кроме опорного. Поэтому рекурсивные вызовы будут производиться для подмассивов размера 0 и $n-1$.

Как и в сортировке слиянием, время, затраченное одним рекурсивным вызовом на $n$-элементном подмассиве, есть $\Theta(n)$. В сортировке слиянием это было время на слияние, а в быстрой сортировке это время на разбиение.

Время выполнения в худшем случае

Если в быстрой сортировке происходят наиболее несбалансированные разбиения, то исходный вызов займет $cn$ времени, где $c$ – константа, рекурсивный вызов для $n-1$ элементов займет $c(n-1)$ времени, рекурсивный вызов для $n-2$ элементов потребует $c(n-2)$ времени и т.д. На рисунке показано дерево размеров подзадач вместе с временем на разбиение:

Рис. 5

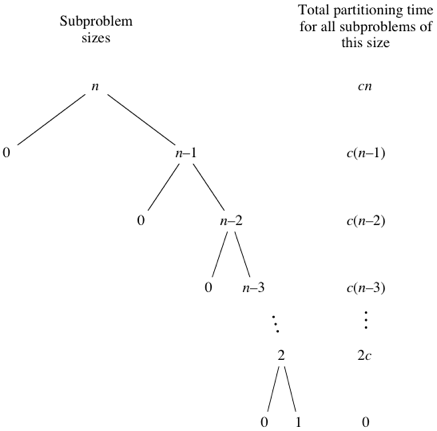
Если сложить время на разбиение на каждом уровне, мы получим

\[cn + c(n-1) + c(n-2) + \dots + 2c =\] \[= c(n + (n-1) + (n-2) + \dots + 2) = c((n+1)(n/2) - 1)\]

по формуле суммы арифметической прогрессии. Таким образом, время выполнения быстрой сортировки в худшем случае есть $\Theta(n^2)$.

Время выполнения в лучшем случае

Лучший случай в быстрой сортировке возникает тогда, когда разбиения максимально сбалансированы: размеры частей подмассива либо равны, либо отличаются на единицу. Первый случай возникает, если в подмассиве нечетное число элементов и опорный элемент находится после разбиения ровно посередине, тогда в каждой части разбиения $(n-1)/2$ элементов. Второй случай возникает, если число элементов в подмассиве $n$ четно и в одной части разбиения $n/2$ элементов, а в другой $n/2 - 1$ элементов. В обоих этих случаях в каждой части разбиения не более $n/2$ элементов, и дерево размеров подзадач очень похоже на дерево размеров подзадач в сортировке слиянием, а время разбиения похоже на время слияния:

Рис. 6

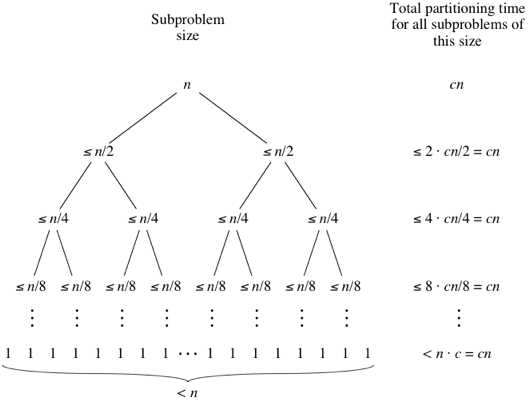
Таким образом, аналогично сортировке слиянием получаем, что время выполнения быстрой сортировки в лучшем случае есть $\Theta(n\log_2 n)$.

Время выполнения в среднем

Чтобы показать, что время выполнения в среднем также равно $\Theta(n\log_2 n)$, нужны сложные математические выкладки, и здесь мы их опустим. Но мы можем достичь некоторого интуитивного понимания, рассмотрев несколько других случаев, чтобы понять, почему время выполнения в среднем может быть $O(n\log_2 n)$. (Отсюда сразу следует, что время выполнения есть $\Theta(n\log_2 n)$, потому что время выполнения в среднем не может быть меньше, чем время выполнения в лучшем случае.) Вначале представим, что у нас не всегда получаются сбалансированные разбиения, но соотношение размеров частей разбиения всегда не хуже, чем 3 к 1. То есть допустим, что в результате каждого разбиения с одной стороны окажется $3n/4$ элементов, а с другой стороны $n/4$ элементов. (Чтобы упростить вычисления, не будем учитывать опорный элемент.) Тогда дерево размеров подзадач и время разбиения будут такими:

Рис. 7

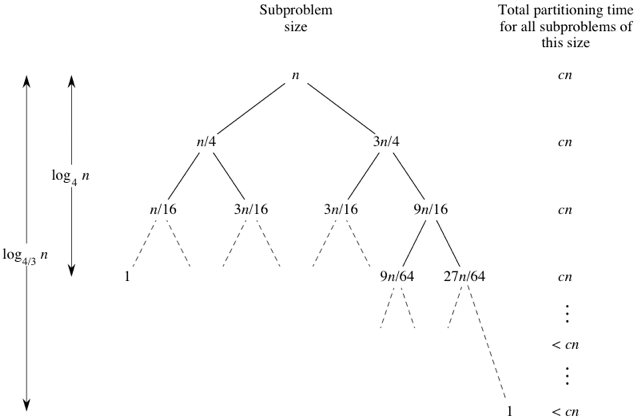
Левый потомок каждого узла дерева соответствует подзадаче размера 1/4 от длины подмассива, а правый потомок соответствует подзадаче размера 3/4 от длины подмассива. Поскольку наименьшие подзадачи находятся слева, то, следуя по левым потомкам, мы спустимся от корня до листа (подзадачи размера 1) быстрее, чем по любому другому пути. Как показано на рисунке, мы спустимся до подзадачи размера 1, пройдя $\log_4 n$ уровней. Почему $log_4 n$ уровней? Удобно рассуждать с конца: начнем с подзадачи размера 1 и будем умножать размер подзадачи на 4 до тех пор, пока не достигнем $n$. Другими словами, нас интересует, при каком значении $x$ будет выполняться равенство $4^x = n$? Ответ: $\log_4 n$. Что будет, если спускаться вниз по правым потомкам? Рисунок показывает, что потребуется $\log_{4/3} n$ уровней, чтобы спуститься до подзадачи размера 1. Почему $\log_{4/3} n$ уровней? Поскольку каждый правый потомок имеет размер 3/4 от размера его родителя, то размер каждого родителя в 4/3 раз больше, чем размер его правого потомка. Снова начнем с подзадачи размера 1 и будем умножать размер подзадачи на 4/3, до тех пор, пока не достигнем $n$. При каком значении $x$ выполняется равенство $(4/3)^x = n$? Ответ: $\log_{4/3} n$.

На каждом из первых $\log_4 n$ уровней находится $n$ узлов (снова не учитываем, что опорные элементы сюда не входят), и поэтому общее время, затраченное на разбиение на каждом из этих уровней, равно $cn$. Но что насчет оставшихся уровней? На каждом из них меньше, чем $n$ узлов, поэтому время разбиения на каждом уровне не более $cn$. Всего у нас $\log_{4/3} n$ уровней, поэтому общее время, затраченное на разбиение, есть $O(n\log_{4/3}n)$. Поскольку

\[\log_a n = \dfrac{\log_b n}{\log_b a}\]

для любых положительных чисел $a$, $b$, $n$, то, полагая $a = 4/3$ и $b = 2$, получим, что

\[\log_{4/3} n = \dfrac{\log_2 n}{\log_2 (4/3)},\]

и поэтому $\log_{4/3}n$ и $\log_2 n$ отличаются только на множитель $\log_2(4/3)$, т.е. на константу. Так как константа не влияет на асимптотику, мы можем сказать, что если на всех разбиениях размеры частей подмассива относятся как 3 к 1, то время выполнения быстрой сортировки есть $O(n\log_2 n)$, хотя и с большим постоянным множителем, чем во времени выполнения в лучшем случае.

Как часто можно ожидать, что части разбиения будут относиться как 3 к 1 или лучше? Это зависит от выбора опорного элемента. Допустим, что опорный элемент после разбиения может оказаться с одинаковой вероятностью в любом месте $n$-элементного подмассива. Тогда для того, чтобы получить разбиение 3 к 1 или лучше, опорный элемент должен быть где-нибудь в “средней половине”:

Рис. 8

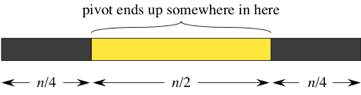
Итак, если опорный элемент может с равной вероятностью оказаться где угодно после разбиения, то есть 50%-ный шанс получить разбиение 3 к 1 или лучше. Другими словами, можно ожидать разбиение не хуже, чем 3 к 1, примерно в половине случаев.

Чтобы понять, почему время выполнения быстрой сортировки в среднем есть $O(n\log_2 n)$, рассмотрим другой случай: что произойдет, если в половине случаев, когда мы не получим разбиение 3 к 1, мы получим наихудшее разбиение? Предположим, что разбиения 3 к 1 и наихудшие разбиения чередуются, и рассмотрим узел дерева, соответствующий подмассиву из $k$ элементов. Тогда часть этого дерева будет выглядеть так:

Рис. 9

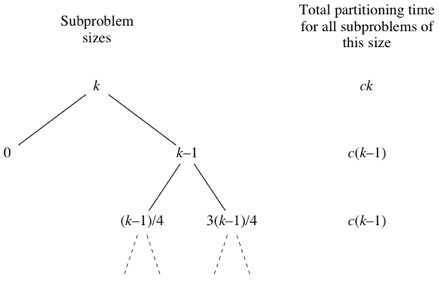
вместо такого дерева:

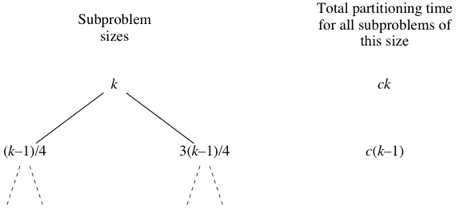
Рис. 10

Следовательно, даже если у нас будет наихудшее разбиение в половине случаев и разбиение не хуже, чем 3 к 1, в другой половине случаев, то время выполнения быстрой сортировки будет примерно в 2 раза больше, чем время выполнения алгоритма, когда каждый раз мы получаем разбиение 3 к 1. Снова замечаем, что это лишь постоянный множитель, который не влияет на асимптотическую оценку, и поэтому в этом случае, когда происходит чередование наихудших разбиений и разбиений 3 к 1, время выполнения есть $O(n\log_2 n)$.

Обращаем внимание, что этот анализ не является математически строгим, но он дает интуитивную идею, почему время выполнения быстрой сортировки в среднем может быть $O(n\log_2 n)$.

Рандомизированная быстрая сортировка

Предположим, что ваш злейший враг дал вам массив, чтобы вы его отсортировали быстрой сортировкой, зная, что вы всегда выбираете самый правый элемент в каждом подмассиве в качестве опорного элемента, и расположил элементы массива таким образом, что вы всегда получаете наихудшее разбиение. Как вам разрушить планы врага?

Вы можете не обязательно выбирать самый правый элемент в каждом подмассиве в качестве опорного. Вместо этого вы можете случайно выбирать элемент в подмассиве и использовать этот элемент в качестве опорного. Но постойте – функция partition предполагает, что опорный элемент находится на самом правом месте в подмассиве. Без проблем – просто поменяйте местами элемент, который вы выбрали в качестве опорного, с самым правым элементом и затем произведите процедуру разбиения, как и раньше. Пока ваш враг не знает, как вы выбираете случайные места в подмассиве, можете спать спокойно.

На самом деле с немного большими усилиями можно повысить шанс получить разбиение, которое будет не хуже, чем 3 к 1. Выберем случайно не один, а три элемента в подмассиве и выберем медиану этих трех элементов в качестве опорного элемента (меняя ее местами с самым правым элементом). Под медианой мы понимаем тот элемент из трех, значение которого находится посередине. Не будем объяснять, почему, но если вы выберете медиану трех случайно выбранных элементов в качестве опорного, то у вас будет шанс 68.75% (11/16), что вы получите разбиение 3 к 1 или лучше. Вы можете пойти дальше. Если вы случайно выберете 5 элементов и возьмете их медиану в качестве опорного элемента, то ваш шанс получить разбиение не хуже, чем 3 к 1, возрастает примерно до 79.3% (203/256). Если вы выберете медиану 7 случайно выбранных элементов, шанс будет около 85.9% (1759/2048). Медиана 9 элементов? Около 90.2% (59123/65536). Медиана 11? Около 93.1% (488293/524288). Ну вы поняли. Конечно, не обязательно нужно случайно выбирать большое число элементов и находить их медиану – ведь время, потраченное на эти действия, может нейтрализовать эффект от получения хороших разбиений в каждом случае.

Время выполнения алгоритма в среднем

Источник: Sedgewick R., Wayne K. Algorithms. Part 1. – P. 293-294.

Докажем, что быстрая сортировка требует в среднем около $2N\ln N$ сравнений при сортировке массива длины $N$, в котором все элементы различны.

Пусть $C_N$ – среднее число сравнений, требуемых для сортировки массива из $N$ элементов с различными элементами. Заметим, что $C_0 = C_1 = 0$. При $N > 1$ получаем рекуррентное соотношение:

\[C_N = (N+1) + (C_0 + C_1 + \dots + C_{N-2} + C_{N-1})/N +\] \[+ (C_{N-1} + C_{N-2} + \dots + C_0)/N.\]

Первое слагаемое – это число операций сравнения при выполнении процедуры разбиения, второе слагаемое – это среднее число операций сравнения при сортировке левого подмассива (который с равной вероятностью имеет длину от 0 до $N-1$), третье слагаемое – это среднее число сравнений при сортировке правого подмассива (такое же, как для левого).

Отсюда

\[NC_N = N(N+1) + 2\sum\limits_{i=0}^{N-1} C_i.\]

Заменяя $N$ на $N-1$, получим

\[(N-1)C_{N-1} = (N-1)N + 2\sum\limits_{i=0}^{N-2} C_i.\]

Вычитая одно равенство из другого, приходим к соотношению

\[NC_N - (N-1)C_{N-1} = 2N + 2C_{N-1},\]

отсюда

\[NC_N = (N+1)C_{N-1} + 2N.\]

Разделим это равенство на $N(N+1)$:

\[\frac{C_N}{N+1} = \frac{C_{N-1}}{N} + \frac{2}{N+1}.\]

Из этого соотношения вытекает, что

\[\frac{C_N}{N+1} = \frac{2}{N+1} + \frac{2}{N} + \dots + \frac{2}{3} + \frac{C_1}{2},\] \[C_N = 2(N+1)\left(\frac{1}{3} + \frac{1}{4} + \dots + \frac{1}{N+1} \right).\]

Выражение в скобках приближенно равно площади под графиком функции $\frac{1}{x}$ от 3 до $N+1$, поэтому $C_N \approx 2N\ln N$.