Метод Ньютона
Метод Ньютона предназначен для решения нелинейных уравнений вида
\[\tag{eq1} f(x) = 0,\]где \(f \colon X \to Y\). Здесь \(X\), \(Y\) могут быть как конечномерными пространствами \(\mathbb R^n\), так и бесконечномерными банаховыми пространствами.
Вначале мы рассмотрим случай \(X = Y = \mathbb R\) (или \(\mathbb C\)), затем случай конечномерных пространств и, наконец, обобщим метод Ньютона на бесконечномерные пространства.
В первом случае задача нахождения корней уравнения (eq1) обычно решается в два этапа. На первом этапе изучается расположение корней (в общем случае на комплексной плоскости) и проводится их разделение, т.е. выделяются области в комплексной плоскости, содержащие только один корень. Кроме того, изучается вопрос о кратности корней. Тем самым находятся некоторые начальные приближения для корней уравнения (eq1). На втором этапе, используя заданное начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня.
Заметим, что если на \((a, b)\) имеется несколько корней, то итерационный процесс может сойтись к одному из корней, но заранее неизвестно, к какому именно. Можно использовать прием выделения корней: если корень \(x = x_*\) кратности \(m\) найден, то рассматривается функция \(g(x) = f(x)/(x-x_*)^m\) и для нее повторяется процесс нахождения корня [Самарский, Гулин, 1989].
Одномерный случай
Метод простой итерации
Метод простой итерации решения уравнения \(x = \varphi(x)\) имеет вид \(x_{n+1} = \varphi(x_n).\)
Условие сходимости данного метода вытекает из принципа сжимающих отображений.
Определение. Оператор \(A\) является сжимающим оператором (сжатием) на \(D\), если существует \(q \in (0,1)\) такое, что для любых \(x_1, x_2 \in D\) выполняется неравенство
\[\|Ax_1 - Ax_2\| \leq q\|x_1 - x_2\|.\]Число \(q\) называется коэффициентом сжатия.
Теорема. [Треногин, 1980] Пусть оператор \(A\) отображает замкнутое в банаховом пространстве \(X\) множество \(D\) в себя и является на \(D\) сжимающим оператором с коэффициентом сжатия \(q\). Тогда в \(D\) оператор \(A\) имеет единственную неподвижную точку $x_*$. Пусть $x_0 \in D$ произвольно. Образуем последовательность
\[x_n = Ax_{n-1},\;\; n = 1, 2, \ldots.\]Тогда \(x_n \in D\) и \(x_n \to x_*\) при \(n \to \infty\). Кроме того, справедлива оценка скорости сходимости
\[\|x_n - x_*\| \leq \frac{q^n}{1-q}\|Ax_0 - x_0\|.\]Получим условие сходимости метода простой итерации решения уравнения
\[\tag{eq2} x = \varphi(x)\]для случая числовой функции \(\varphi\).
Предположим, что уравнение (eq2) имеет корень \(x = x_*\) и в круге \(B = \{x \colon |x-x_*| \leq r\}\) функция \(\varphi(x)\) непрерывна по Липшицу с постоянной \(q \in (0,1)\):
\[\varphi(x_1) - \varphi(x_2) \leq q|x_1 - x_2|\]для любых точек \(x_1, x_2 \in B\).
Теорема. [Березин, Жидков, 1959] Каково бы ни было \(x_0 \in B\), последовательность \(x_k = \varphi(x_{k-1})\) \((k = 1, 2, \ldots)\) сходится к \(x_*\), если только \(\varphi(x)\) в круге \(B\) удовлетворяет условию Липшица с константой \(q < 1\), причем скорость сходимости характеризуется неравенством
\[|x_n - x_*| \leq q^n|x_0 - x_*|.\]Доказательство. Если \(x \in B\), то \(y = \varphi(x)\) также принадлежит \(B\), так как
\[|y - x_*| = |\varphi(x) - \varphi(x_*)| \leq q|x - x_*| < r.\]Таким образом, отображение \(\varphi\) отображает круг \(B\) в себя. Кроме того, \(\varphi(x)\) — сжимающее отображение, поскольку для любых \(x, y \in B\):
\[|\varphi(x) - \varphi(y)| \leq q|x - y|, \quad q < 1.\]Поэтому по принципу сжимающих отображений в \(B\) существует одна и только одна неподвижная точка, но эта точка \(x = x_*\). Эту точку можно получить как предел последовательности \(x_k = \varphi(x_{k-1})\) при любом \(x_0 \in B\).
Используя условие Липшица, имеем:
\[|x_n - x_*| = |\varphi(x_{n-1}) - \varphi(x_*)| \leq q|x_{n-1} - x_*|,\]т.е.
\[|x_n - x_*| \leq q|x_{n-1}-x_*| \leq q^2|x_{n-2}-x_*| \leq \ldots \leq q^n|x_0 - x_*|.\]Таким образом, \(x_n\) сходится к \(x_*\) со скоростью геометрической прогрессии со знаменателем \(q\).
Метод Ньютона
Метод Ньютона называется также методом касательных или методом линеаризации. Если \(x_n\) — некоторое приближение к корню \(x_*\), а \(f(x)\) имеет непрерывную производную, то уравнение (eq1) можно преобразовать следующим образом:
\[0 = f(x) = f(x_n + (x_* - x_n)) = f(x_n) + (x_* - x_n)f'(\xi).\]Приближенно заменим \(f'(\xi)\) на значение в известной точке \(x_n\):
\[f(x_n) + (x_* - x_n)f'(x_n) \approx 0.\]Заменим в этом соотношении \(x_*\) на неизвестное следующее приближение:
\[f(x_n) + (x_{n+1} - x_n)f'(x_n) = 0.\]Таким образом, получаем итерационный процесс:
\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.\]Геометрически этот процесс означает замену на каждой итерации графика \(y = f(x)\) касательной к нему.
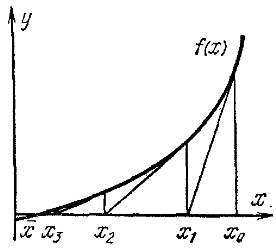
Метод Ньютона можно рассматривать как частный случай метода простой итерации, если положить \(\varphi(x) = x - \frac{f(x)}{f'(x)}.\) Тогда \(\varphi'(x) = 1 - \frac{(f'(x))^2 - f(x)f''(x)}{(f'(x))^2} = \frac{f(x)f''(x)}{(f'(x))^2}.\) Следовательно, \(\varphi'(x_*) = 0\). Отметим, что это верно только для простого корня, для которого \(f'(x_*) \neq 0\). Вблизи \(p\)-кратного корня \(f(x) \approx a(x-x_*)^p\), и \(\varphi'(x_*) = (p-1)/p\), т.е. \(0 \leq \varphi'(x) < 1\) [Калиткин, 1978].
Отсюда следует, что если \(x_*\) — простой корень и \(f\) имеет 2-ю непрерывную производную (в этом случае \(\varphi'(x)\) непрерывна), то \(|\varphi'(x)| < 1\) в окрестности корня \(x_*\). Поэтому при выборе начального приближения в указанной окрестности метод Ньютона сходится. Если всюду \(|ff''| < (f')^2\), то итерации сходятся при произвольном нулевом приближении.
Однако следствием малости \(\varphi'(x)\) в окрестности \(x_*\) является не просто сходимость, а сходимость существенно более быстрая, чем в общем случае метода простой итерации. В следующей теореме доказано, что метод Ньютона имеет квадратичную сходимость, т.е. что он сходится и погрешность на \((k+1)\)-й итерации пропорциональна квадрату погрешности на \(k\)-й итерации.
Теорема. [Самарский, Гулин, 1989] Пусть \(x_*\) — простой вещественный корень уравнения (eq1) и пусть \(f'(x) \neq 0\) в окрестности \(B = \{x \colon |x - x_*| < r\}\). Предположим, что \(f''(x)\) непрерывна в \(B\) и
\[0 < m_1 = \inf_{x\in B}|f'(x)|, \;\; M_2 = \sup_{x \in B}|f''(x)|,\]причем
\[\frac{M_2|x_0 - x_*|}{2m_1} < 1.\]Тогда если \(x_0 \in B\), то метод Ньютона
\[x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)},\;\; k = 0,1,\ldots\]сходится, причем для погрешности справедлива оценка
\[|x_k - x_*| \leq q^{2^k - 1}|x_0 - x_*|,\]где
\[q = \frac{M_2|x_0 - x_*|}{2m_1} < 1.\]Доказательство. Приведем более простые, чем в [Самарский, Гулин, 1989], рассуждения [Березин, Жидков, 1959; Жидков, 2013]. По формуле Тейлора
\[0 = f(x_*) = f(x_n) + f'(x_n)(x_* - x_n) + \frac{1}{2}f''(\xi)(x_* - x_n)^2,\]где \(\xi\) заключено между \(x_*\) и \(x_n\). Отсюда
\[f(x_n) = -f'(x_n)(x_* - x_n) - \frac{f''(\xi)}{2}(x_* - x_n)^2,\] \[\frac{f(x_n)}{f'(x_n)} = x_n - x_* - \frac{1}{2}\frac{f''(\xi)}{f'(x_n)}(x_*-x_n)^2.\]Следовательно,
\[x_{n+1} - x_* = x_n - x_* - \frac{f(x_n)}{f'(x_n)} = \frac{1}{2}\frac{f''(\xi)}{f'(x_n)}(x_*-x_n)^2,\] \[|x_{n+1} - x_*| \leq \frac{M_2}{2m_1}|x_n - x_*|^2.\]Поэтому
\[|x_1 - x_*| \leq \frac{M_2}{2m_1}|x_0 - x_*|^2 = q|x_0 - x_*|,\] \[|x_2 - x_*| \leq \frac{M_2}{2m_1}|x_1 - x_*|^2 \leq \frac{M_2}{2m_1}q^2|x_0 - x_*|^2 = q^3|x_0 - x_*|\]и так далее.
Кратные корни
Говорят, что \(x_*\) является корнем кратности \(p\), если
\[f(x_*) = f'(x_*) = \ldots = f^{(n-1)}(x_*) = 0,\;\; f^{(p)} \neq 0.\]Будем предполагать, что $f^{(p+1)}$ непрерывна в окрестности корня $x_*$ кратности $p$. В случае корня кратности $p$ квадратичную сходимость имеет метод Ньютона с параметром
\[\tag{newton2} f'(x_k)\frac{x_{k+1} - x_k}{p} + f(x_k) = 0.\]Теорема. [СамарскийГулин] Пусть $x_*$ — корень кратности $p$ уравнения (eq1) и в окрестности \(B = \{x \colon |x-x_*| < r\}\) производная $f^{(p)}(x)$ отлична от нуля.
Пусть $f^{(p+1)}$ непрерывна в $B$ и \(0 < m_p = \inf_{x\in B}|f^{(p)}(x)|,\;\;M_{p+1} = \sup_{x\in B}|f^{(p+1)}(x)|,\) причем \(\frac{M_{p+1}|x_0-x_*|}{m_p p(p+1)} < 1.\) Тогда если $x_0 \in B$, то метод (newton2) сходится, причем для погрешности справедлива оценка \(|x_k - x_*| \leq q^{2^k-1}|x_0 - x_*|,\) где \(q = \frac{M_{p+1}|x_0-x_*|}{m_p p(p+1)} < 1.\)
Доказательство.
Из (newton2) получаем \(x_{k+1} = x_k - \frac{pf(x_k)}{f'(x_k)},\)
\[\tag{f1} x_{k+1} - x_* = x_k - x_* - \frac{pf(x_k)}{f'(x_k)} = \frac{(x_k - x_*)f'(x_k) - pf(x_k)}{f'(x_k)} = \frac{F(x_k)}{f'(x_k)},\]где $F(x) = (x-x_*)f’(x) - pf(x)$.
\[F'(x) = (x-x_*)f''(x) + (1-p)f'(x),\] \[F''(x) = (x-x_*)f'''(x) + (2-p)f''(x),\] \[F^{(m)}(x) = (x-x_*)f^{(m+1)}(x) + (m-p)f^{(m)}(x),\] \[F^{(m)}(x_*) = 0,\;\; m = 0, 1, \ldots, p.\]Применим формулу Тейлора с остаточным членом в интегральной форме.
\[F(x_k) = F(x_*) + F'(x_*)(x-x_*) + \frac{1}{2}F''(x_*)(x-x_*)^2 + \ldots + \frac{1}{(p-1)!}F^{(p-1)}(x)(x-x_*)^{p-1} +\] \[+ \frac{1}{(p-1)!}\int_{x_*}^{x_k}(x_k-t)^{p-1}F^{(p)}(t)dt = \frac{1}{(p-1)!}\int_{x_*}^{x_k}(t-x_*)(x_k-t)^{p-1}f^{(p+1)}(t)dt.\]Так как \((t-x_*)(x_k-t)^{p-1} \geq 0\), то мы можем применить формулу среднего значения с обобщенной форме [Ильин, Позняк, с. 350].
\[F(x_k) = \frac{1}{(p-1)!}f^{(p+1)}(\xi_k^{(1)}) \int_{x_*}^{x_k}(t-x_*)(x_k-t)^{p-1}dt.\] \[\int_{x_*}^{x_k}(t-x_*)(x_k-t)^{p-1}dt = -\int_{x_*}^{x_k}(x_k-t)^p dt + (x_k-x_*)\int_{x_*}^{x_k}(x_k-t)^{p-1}dt =\] \[= \left.\frac{(x_k-t)^{p+1}}{p+1}\right|_{x_*}^{x_k} - (x_k - x_*)\left.\frac{(x_k-t)^p}{p}\right|_{x_*}^{x_k} =\] \[= -\frac{(x_k - x_*)^{p+1}}{p+1} + \frac{(x_k-x_*)^{p+1}}{p} = \frac{(x_k - x_*)^{p+1}}{p(p+1)}.\]Следовательно, \(F(x_k) = \frac{f^{(p+1)}(\xi_k^{(1)})}{(p+1)!}(x_k - x_*)^{p+1}.\)
Для оценки знаменателя формулы (f1) применим формулу Тейлора с остаточным членом в форме Лагранжа.
\(f'(x_k) = f'(x_*) + f''(x_*)(x_k - x_*) + \frac{1}{2}f'''(x_*)(x_k - x_*)^2 + \ldots + \frac{1}{(p-1)!}f{(p)}(\xi_k^{(2)})(x_k - x_*)^{p-1} =\) \(= \frac{(x_k - x_*)^{p-1}}{(p-1)!}f^{(p)}(\xi_k^{(2)}).\)
Из (f1) получаем \(|x_{k+1} - x_*| = \left|\frac{F(x_k)}{f'(x_k)}\right| = \left|\frac{f^{(p+1)}(\xi_k^{(1)})(x_k - x_*)^{p+1}(p-1)!} {(p+1)!(x_k - x_*)^{p-1}f^{(p)}(\xi_k^{(2)})} \right| =\) \(\frac{1}{p(p+1)}\frac{|f^{(p+1)}(\xi_k^{(1)})|}{|f^{(p)}(\xi_k^{(2)})|} (x_k - x_*)^2 \leq \frac{M_{p+1}}{m_p p(p+1)}(x_k - x_*)^2.\)
Диагностика кратности и условие остановки
Пусть $p$ — корень кратности $p$, а функция имеет $p$ непрерывных ограниченных производных. Тогда вблизи корня $x_*$ справедливы следующие представления:
\[\tag{pr1} f(x) \approx a(x - x_*)^p, \quad f'(x) \approx pa(x-x_*)^{p-1}.\]Обозначим отклонение от корня $\Delta_k = x_k - x_*$.
\[x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)},\] \[x_{k+1} - x_* = x_k - x_* - \frac{f(x_k)}{f'(x_k)}.\]Подставим представление (pr1):
\[x_{k+1} - x_* \approx x_k - x_* - \frac{1}{p}(x_k - x_*),\]отсюда \(\Delta_{k+1} \approx \left(1 - \frac{1}{p}\right)\Delta_k.\)
Знаменатель геометрической прогрессии можно приближенно определить из следующего соотношения:
\[\tag{znam} q \approx q_k \equiv \frac{x_{k+1} - x_k}{x_k - x_{k-1}}.\]Когда итерации приближаются к корню, $q_k \to q$. Если мы визуально наблюдаем стремление $q_k$ к некоторому пределу $q$, то по величине этого предела нетрудно восстановить кратность корня: \(p \approx 1/(1-q_k).\) Эта формула применима как для кратного корня, так и для простого. Дополнительный контроль: полученное $p$ должно быть очень близким к целому числу.
В силу квадратичной сходимости в случае простого корня можно останавливать итерации по условию
\[|x_{k+1} - x_k| < \varepsilon|x_{k+1}|,\;\;\varepsilon \approx 10^{-10},\]величина $|x_{k+1}|$ в правой части поставлена для того, чтобы $\varepsilon$ соответствовала относительной точности получаемого числа. Это обеспечивает 15–20 верных знаков в значении очередного приближения $x_{k+1}$.
Для кратного корня погрешность очередного приближения можно оценить как сумму геометрической прогрессии, состоящей из еще не сделанных итераций. Это дает следующий критерий остановки итераций:
\[\frac{q}{1-q}(x_{k+1} - x_k) < \varepsilon|x_{k+1}|,\]где $\varepsilon$ — требуемая относительная точность, а $q$ вычисляется по (znam). Однако здесь использование $\varepsilon \approx 10^{-10}$ дает именно такую точность, а не 15–20 верных знаков, как в случае простого корня.
Материал взят из [Калиткин, 2013].
Односторонние приближения
Сходимость вблизи любого корня монотонна, что легко видеть на рисунке; но вдали от корня возможна немонотонность итераций. Отметим, что рисунок указывает еще на одно достаточное условие сходимости итераций. Пусть $f’‘(x) \geq 0$ справа от корня на отрезке \([x_*, a]\); если \(x_0\) выбрано также справа от корня на этом отрезке, то итерации сходятся, причем монотонно. То же будет, если $f’‘(x) \leq 0$ слева от корня на отрезке \([b, x_*]\), и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой $f(x)f’‘(x) \geq 0$ [Калиткин, 1978].
Теорема. Пусть для всех $x \in [a,b]$ либо \(\tag{usl1} f'(x) > 0, f''(x) > 0,\)
либо
\[\tag{usl2} f'(x) < 0, f''(x) < 0.\]Тогда последовательность ${x_k}$, определенная согласно методу Ньютона с $x_0 = b$, монотонно убывает и сходится к $x_*$.
Теорема. Пусть для всех $x \in [a,b]$ либо
\[f'(x) > 0, f''(x) < 0,\]либо
\[f'(x) < 0, f''(x) > 0.\]Тогда последовательность ${x_k}$, определенная согласно методу Ньютона с $x_0 = a$, монотонно возрастает и сходится к $x_*$.
Доказательство 1-й теоремы. Предположим, что для некоторого $k \geq 0$ выполняются неравенства \(x_* < x_k \leq b\) и докажем, что тогда \(\tag{d1} x_* < x_{k+1} < x_k.\)
Перепишем уравнение метода Ньютона в виде
\[x_k - x_{k+1} = \frac{f(x_k) - f(x_*)}{f'(x_k)}\]и воспользуемся формулой конечных приращений Лагранжа. Тогда получим
\[\tag{p1} x_k - x_{k+1} = \frac{(x_k - x_*)f'(\xi_k)}{f'(x_k)},\]где \(\xi_k \in (x_*, x_k)\).
Пусть выполнено условие (usl1). Тогда \(0 < \frac{f'(\xi_k)}{f'(x_k)} < 1\), причем последнее неравенство является следствием монотонного возрастания $f’(x)$. Те же самые неравенства выполняются в случае условий (usl2). Таким образом, \(0 < \frac{(x_k - x_*)f'(\xi_k)}{f'(x_k)} < x_k - x_*,\) и из (p1) получим \(0 < x_k - x_{k+1} < x_k - x_*,\) т.е. получим требуемые неравенства (d1). Таким образом, последовательность ${x_k}$ монотонно убывает и ограничена снизу числом \(x_*\). Поэтому данная последовательность имеет предел, который в силу непрерывности функции $f(x)$ и условия $f’(x_*) \neq 0$ совпадает с корнем \(x_*\) уравнения (eq1). Теорема доказана.
Многомерный случай
Пусть известно некоторое приближение \(x^{(s)}\) к корню \(x_*\). Как и для одной переменной, запишем исходную систему (eq1) в виде $f(x^{(s)} + \Delta x) = 0$, где $\Delta x = x_* - x^{(s)}$. Разлагая эти уравнения в ряды и ограничиваясь первыми дифференциалами, т.е. линеаризуя функцию, получим \(\sum_{i=1}^n\frac{\partial f_k(x^{(s)})}{\partial x_i}\Delta x_i^{(s)} = -f_k(x^{(s)}),\quad 1 \leq k \leq n.\) Это система уравнений, линейных относительно приращений $\Delta x_i^{(s)}$; все коэффициенты этой системы выражаются через последнее приближение $x^{(s)}$. Решив эту систему, найдем новое приближение \(x^{(s+1)} = x^{(s)} + \Delta x^{(s)}.\)
Как и для одной переменной, метод Ньютона можно формально свести к методу последовательных приближений, положив $\varphi(x) = x - [\partial f/\partial x]^{-1}f(x)$, где $[\partial f/\partial x]^{-1}$ есть матрица, обратная матрице производных. Аналогично проводится теоретический анализ условий сходимости. В достаточнно малой окрестности корня итерации сходятся, если $\det[\partial f/\partial x] \neq 0$, причем сходимость квадратичная.
Для метода Ньютона хорошим критерием окончания итераций является условие $|x^{(s)} - x^{(s+1)}| \leq \varepsilon$. В самом деле, вблизи корня ньютоновские итерации сходятся квадратично, поэтому если этот критерий выполнен, то $|x^{(s)} - x^{(s+1)}| \approx \varepsilon^2 « \varepsilon$. Выбирая $\varepsilon \approx 10^{-5} - 10^{-6}$, можно получить решение с десятком верных знаков.
Теорема. [СамарскийГулин] Предположим, что в \(B = \{x \in \mathbb R^m \colon \|x - x^0\| < r\) матрица $f’(x)$ удовлетворяет условию Липшица с постоянной $L$, т.е. \(\|f'(x^1) - f'(x^2)\| \leq L\|x^1 - x^2\|\) для любых $x^1, x^2 \in B$. Пусть в $B$ матрица $[f’(x)]^{-1}$ существует, причем элементы ее непрерывны и \(\|[f'(x)]^{-1}\| \leq M.\)
Если начальное приближение $x^0$ таково, что $|f(x^0)| \leq \eta$ и \(q = \frac{M^2L\eta}{2} < 1,\) причем \(M\eta\sum_{k=0}^\infty q^{2^k - 1} < r,\) то система уравнений (eq1) имеет решение $x_* \in B$, к которому сходится метод Ньютона. Оценка погрешности дается равенством \(\|x^k - x_*\| \leq M\eta\frac{q^{2^k-1}}{1 - q^{2^k}}.\)
Бесконечномерный случай
Пусть $G \colon X \to Y$, $X, Y$ — банаховы пространства. Рассмотрим операторное уравнение \(G(x) = 0.\) Предположим, что $G$ непрерывно дифференцируем по Фреше.
Метод Ньютона: \(x^{k+1} = x^k - [G'(x^k)]^{-1}G(x^k).\)
Условие регулярности: \(\|[G'(x^k)]^{-1}\| \leq C \;\; \forall k \geq 0.\) Это будет выполняться, если $G’$ непрерывна в точке $x_$ и $G’(x_)$ непрерывно обратим [@Pinnau].
Из дифференцируемости по Фреше следует, что \(\|G(x_* + d^k) - G(x_*) - G'(x_*)d^k\|_Y = o(\|d^k\|_X).\) Далее, в силу непрерывности $G’$:
\(\|G(x_* + d^k) - G(x_*) - G'(x^k)d^k\|_Y = \|G(x_* + d^k) - G(x_*) - G'(x_* + d^k)d^k\|_Y \leq\) \(\leq \|G(x_* + d^k) - G(x_*) - G'(x_*)d^k\|_Y + \leq \|(G'(x_*) - G'(x_* + d^k))d^k\|_Y \leq\) \(\leq o(\|d^k\|_X) + \|G'(x_*) - G'(x_* + d^k)\|\|d^k\|_X = o(\|d^k\|_X)\)
при \(\|d^k\|_X \to 0\). Мы доказали сверхлинейное условие приближения.
Если $G’$ удовлетворяет условию Гельдера порядка $\alpha$ вблизи $x_*$, можно получить условие приближения порядка $1 + \alpha$: \(\|G(x_* + d^k) - G(x_*) - G'(x^k)d^k\|_Y = O(\|d^k\|_X^{1+\alpha}).\)
Тогда \(\|x^{k+1} - x_*\|_X = \|d^{k+1}\|_X = \|[G'(x_k)]^{-1}(G(x_* + d^k) - G(x_*) - G'(x^k)d^k)\|_X = O(\|d^k\|_X^{1+\alpha}).\) Следовательно, метод Ньютона сходится с порядком $1 + \alpha$. Если $G’$ удовлетворяет условию Липшица, то $\alpha = 1$ и сходимость квадратичная.
Заключение
Отметим основные особенности метода Ньютона.
-
Метод Ньютона годится не только для скалярных уравнений, его можно обобщить на произвольные банаховы пространства.
-
Метод имеет квадратичную сходимость, т.е. погрешность на следующей итерации пропорциональна квадрату погрешности на предыдущей итерации: $x_{n+1} - x_* = O((x_k - x_*)^2)$.
-
Такая быстрая сходимость метода Ньютона гарантируется только при очень хороших, т.е. близких к точному решению, начальных приближениях. Если начальное приближение выбрано неудачно, то метод может сходиться медленно, либо не сойдется вообще.
Список литературы
Березин И.С., Жидков Н.П. Методы вычислений. Т. 2. М.: Наука, 1959.
Жидков Е.Н. Вычислительная математика: учебник для студ. учреждений высш. проф. образования. М.: Издательский центр “Академия”, 2013.
Ильин В.А., Позняк Э.Г. Основы математического анализа: В 2-х ч. Часть I: Учеб.: Для вузов. М.: ФИЗМАТЛИТ, 2008.
Калиткин Н.Н. Численные методы. М: Наука, 1978.
Калиткин Н.Н., Альшина Е.А. Численный анализ: учебник для студ. учреждений высш. проф. образования. М.: Издательский центр “Академия”, 2013.
Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. М.: Наука, 1989.
Самарский А.А., Гулин А.В. Численные методы математической физики. М.: Научный мир, 2000.
Треногин В.А. Функциональный анализ. М.: Наука, 1980.
Hinze M., Pinnau R., Ulbrich M, Ulbrich S. Optimization with PDE constraints. Springer, 2009.