Сортировка

Под временной сложностью алгоритма понимают функцию $T(n)$ от размерности входных данных $n$, равную наибольшему времени работы алгоритма на входных данных размерности $n$. Размерность входных данных – это мера их количества, она может быть задана несколькими числами.

Эффективность алгоритма зависит от того, как быстро растет $T(n)$ с ростом $n$. Основным показателем временной сложности алгоритма служит асимптотическая скорость увеличения времени работы алгоритма при $n \to \infty$. Например, если временная сложность – это полином $T(n) = an^p + bn^{p-1} + cn + d$, то при больших $n$ слагаемое со старшей степенью $n^p$ будет значительно больше, чем все другие слагаемые, и поэтому порядок скорости роста $T(n)$ характеризует эффективность алгоритма при больших $n$.

Говорят, что $T(n)$ – бесконечно большая функция менее высокого порядка, чем $f(n)$, если $T(n) \leq Cf(n)$, начиная с некоторого $n = n_0$. В этом случае пишут $T(n) = O(f(n))$, подразумевая под $O(f(n))$ класс функций, а равенство в этой формуле обозначает принадлежность функции этому классу.

Задача сортировки заключается в переупорядочении последовательности ключей $a_1, a_2, \ldots, a_n$ (к которой привязаны блоки данных) так, чтобы $a_1’ \leq a_2’ \leq \ldots \leq a_n’$.

Если процедура сортировки опирается только на операцию сравнения двух значений ключей, в результате которой можно сказать, что одно ключевое значение меньше другого, то временная сложность имеет порядок роста не лучше, чем $O(n\log n)$. Можно нарисовать двоичное дерево, в котором узлы будут соответствовать некоторым упорядочениям данных после определенного количества сделанных сравнений ключей. В каждом узле, кроме листьев, программа определяет порядок данных посредством сравнения каких-либо двух элементов, например: “является ли $k_1 < k_2$?”. В зависимости от возможных ответов на этот вопрос создаются два сына этого узла. Левый сын соответствует случаю, когда значения ключей удовлетворяют неравенству $k_1 < k_2$; правый сын соответствует упорядочению при выполнении неравенства $k_1 > k_2$.

Поскольку всего возможных порядков следования элементов $n!$, то в этом дереве всего $n!$ листьев. Высота дерева равна $\log_2(n!)$, так что время выполнения алгоритма сортировки оценивается сверху величиной $O(\log(n!)) = O(n\log n)$.

Сортировка вставками, сортировка выбором

В сортировке вставками все элементы массива просматриваются слева направо, и на каждой итерации цикла поддерживается инвариант: подмассив $A[1..i-1]$ содержит те же элементы, что и в исходном массиве $[1..i-1]$, но в отсортированном порядке. Для обеспечения инварианта элемент $A[i]$ перемещается на позицию $j$ в подмассиве $A[1..i]$, такую, что $j = \max{j \in 1..i \colon A[i] \geq A[j-1]}$, здесь $A[0] = -\infty$. Эта запись означает, что $A[j-1] \leq A[i] < A[j]$ (либо $j = i$ и правое неравенство переходит в равенство).

\({\tt InsertionSort} (@A[1..n]) = \{\)
$\qquad$ \({\bf for}\; i \leftarrow 2..n\; \{\)
$\qquad\qquad$ // $A[1..i-1]$ отсортирован
$\qquad\qquad$ \(j = \max\{j \in 1..i \colon A[i] \geq A[j-1]\} = \{\)
$\qquad\qquad\qquad$ \(j \leftarrow i\)
$\qquad\qquad\qquad$ \({\bf while}\; j > 1 \;\text{и}\; A[i] < A[j-1] \; \{\)
$\qquad\qquad\qquad\qquad$ \(j \leftarrow j - 1\)
$\qquad\qquad\qquad$ \(\}\)
$\qquad\qquad$ \(\}\)
$\qquad\qquad$ вставить $A[i]$ в позицию $j$
$\qquad\qquad$ // $A[1..i]$ отсортирован
$\qquad$ \(\}\)

В [Скиена, с. 21] поиск индекса $j$ и вставка элемента объединены в один цикл с перестановкой соседних элементов.

Если сортировка вставками выбирает место, куда вставить данный элемент массива, то сортировка выбором выбирает для каждой позиции в массиве, начиная с минимальной, соответствующий элемент. На каждом шаге выбирается наименьший элемент из оставшихся, который помещается в очередной элемент массива.

void sort (int n, int A[])
{
   for (int i = 0; i < n; ++i) {
      // подмассив A[0..i-1] отсортирован
      //   и содержит i наименьших элементов массива A[0..n-1]

      // в подмассиве A[i..n-1] выбираем наименьший элемент
      // и складываем результат в A[i]
      for (int j = i + 1; j < n; ++j) {
         if (A[i] > A[j])
            swap(A[i], A[j]);
      }

      // подмассив A[0..i] отсортирован
   }
}

Оба рассмотренных алгоритма имеют временную сложность $O(n^2)$, поэтому их можно использовать, когда число $n$ не слишком велико.

Сортировка слиянием

Рекурсивные алгоритмы разбивают большую задачу на несколько подзадач. При рекурсивном подходе сортируемые элементы разбиваются на две группы, каждая из этих меньших групп сортируется рекурсивно, после чего два отсортированных списка сливаются воедино, и их элементы чередуются, образуя полностью отсортированный общий список. Этот алгоритм называется сортировкой слиянием (mergesort).

Mergesort(A[1,n]) 
Merge( MergeSort(A[1, [n/2]), Mergesort(A[[n/2] + 1,n]) ) 

Базовый случай рекурсивной сортировки имеет место, когда исходный массив состоит из одного элемента, вследствие чего перестановки в нем невозможны. На рисунке показана графическая иллюстрация работы алгориГма сортировки слиянием; Сортировку слиянием можно представлять себе как симметричный обход верхнего дерева, при котором преобразования представлены в нижнем (перевернутом) дереве.

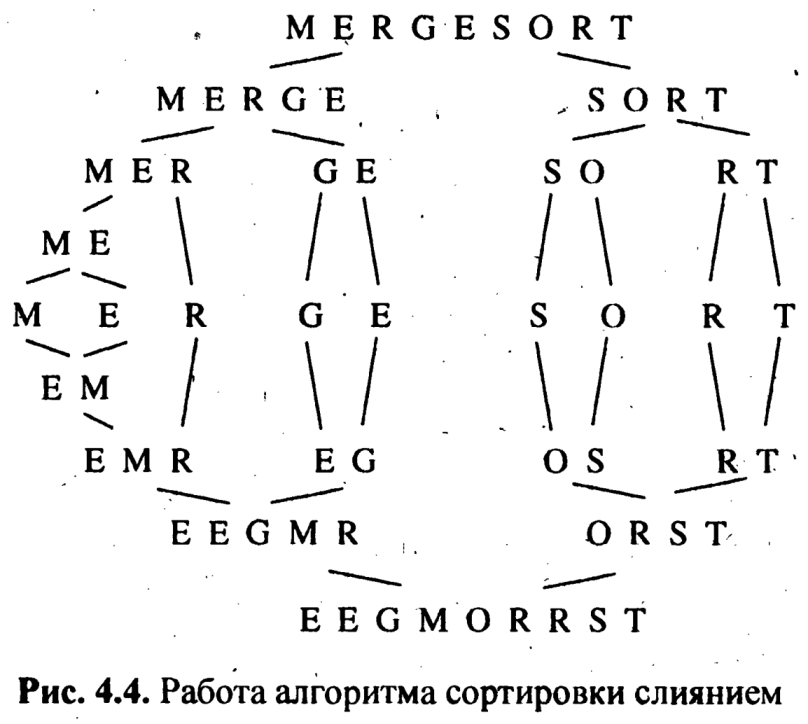
Заметим, что подпрограмма сортировки дважды вызывает саму себя с глубиной рекурсии порядка $\log_2 n$. Суммарное количество сравнений на каждой глубине рекурсии равно $O(n)$. Таким образом, сортировка слиянием потребует порядка $O(n\log n)$ операций.

Алгоритм сортировки слиянием хорошо подходит для сортировки связных списков, т. к. он, в отличие от алгоритмов пирамидальной и быстрой сортировки, не основывается на произвольном доступе к элементам. Его основным недостатком является необходимость во вспомогательном буфере при сортировке массивов. Отсортированные связные списки можно легко слить вместе, не требуя дополнительной памяти, а просто упорядочивая указатели. Но для влияния двух отсортированных массивов (или частей массива) требуется третий массив для хранения результатов слияния, чтобы не потет рять содержимое сливаемых массивов. Допустим, что мы сливаем множества {4, 5, 6} и {1,2, 3}., записанные слева направо в одном массиве. Без использования буфера нам придется записывать отсортированные элементы поверх элементов первой половины массива, вследствие чего последние будут утеряны.

Сортировка слиянием является классическим примером алгоритмов типа “разделяй и властвуй”. Мы всегда в выигрыше, когда можем разбить одну большую задачу на две подзадачи, т. к. меньшие задачи легче решить. Секрет заключается в том, чтобы воспользоваться двумя частичными решениями для создания решения всей задачи, как это было сделано с операцией слияния.

Быстрая сортировка

Алгоритм быстрой сортировки имеет в наихудшем случае для входного массива из $n$ элементов время работы, равное $O(n^2)$. Несмотря на такую медленную работу в наихудшем случае, этот алгоритм на практике зачастую оказывается оптимальным благодаря тому, что в среднем время его работы намного лучше: $O(n\log n)$. Кроме того, постоянный множитель, скрытый в выражении $O(n\log n)$, достаточно мал по величине.

Быстрая сортировка, подобно сортировке слиянием, применяет парадигму “разделяй и властвуй”.

Разделение. Массив $А[р..r]$ разбивается на два (возможно, пустых) подмассива $А[р..q-1]$ и $A[q+1..r]$, таких, что каждый элемент $А[р..q — l]$ меньше или равен $A[q]$, который, в свою очередь, не превышает любой элемент подмассива $A[q + 1..r]$. Индекс $q$ вычисляется в ходе процедуры разбиения.

Обработка. Подмассивы $А[р..q — 1]$ и $A[q + 1..r]$ сортируются с помощью рекурсивного вызова процедуры быстрой сортировки.

Комбинирование. Поскольку подмассивы сортируются на месте, для их объединения не требуются никакие действия: весь массив $А[р..r]$ оказывается отсортированным.

Быстрая сортировка реализуется следующей процедурой.

\({\tt Quicksort}({\tt @}A[p..r]) = \{\)
$\qquad$ \({\bf if}\; р < r\;\; \{\)
$\qquad\qquad$ \(q \leftarrow {\tt Partition} ({\tt @}A[p..r])\)
$\qquad\qquad$ \({\tt Quicksort}({\tt @}A[p..q - 1])\)
$\qquad\qquad$ \({\tt Quicksort}({\tt @}A[q + 1,r])\)
\(\}\)

Разбиение проводится процедурой, описанной здесь, а также [КЛРШ, с. 199].

Инвариант цикла: $p \leq q \leq j$, и подмассив $A[p..j-1]$ разбивается на 2 подмассива: $A[p..q-1] \leq A[r]$, $A[q..j-1] > A[r]$.

В среднем алгоритм быстрой сортировки работает быстрее, чем сортировка слиянием и пирамидальная сортировка в связи с тем, что при хранении промежуточных результатов алгоритм быстрой сортировки накладывает более гибкие требования, и поэтому для поддержания этих условий потребуется меньшее число операций.

Инициализация. При $j = p$ подмассив $A[p..j-1]$ пуст, поэтому инвариант выполняется.

Сохранение. Чтобы обеспечить инвариант на $j$-й итерации цикла, сравним $A[r]$ с $A[j]$. Если $A[r] < A[j]$, то подмассив $A[p..q-1] \leq A[r]$, остается на месте, и $A[q..j] > A[r]$. А если $A[j] \leq A[r]$, то первый элемент второго подмассива перемещаем в конец, $A[q] \leftrightarrow A[j]$, а $A[j]$ помещаем в конец первого подмассива.

В первом случае $A[r] < A[j]$ граница подмассивов и первый подмассив остаются прежними, и новое логическое условие $A[p..q-1] \leq A[r]$ выполняется, а также $A[q..j] > A[r]$. Во втором случае $A[j] \leq A[r]$ имеем $A’[p..q’-1] = A’[p..q] \leq A’[r]$ (так как $A’[q] = A[j] \leq A[r] = A’[r]$); $A’[q’..j] > A’[r]$, где $A’[q’..j] = A[q+1..j-1] \times A[q] > A[r]$.

Завершение. При $j = r$, после окончания выполнения цикла инвариант сохраняется, так что $p \leq q \leq r$, $A[p..q-1] \leq A[r]$, $A[q..r-1] > A[r]$.

Теперь поменяем местами $A[r] \leftrightarrow A[q]$, получим искомое разбиение массива $A[p..r]$ на два подмассива $A[p..q-1]$, $A[q]$, $A[q+1..r]$ (возможно, пустых), таких, что $A[p..q-1] \leq A[q]$, $A[q+1..r] > A[q]$, здесь $p \leq q \leq r$.

Здесь в качестве опорного элемента в процедуре Partition мы выбрали самый правый элемент. В таком случае можно подобрать набор тестов, на котором быстрая сортировка будет давать асимптотику $O(n^2)$. Для исключения плохих случаев применяют рандомизированные алгоритмы. А именно, поменяем самый правый элемент со случайным элементом. Либо выберем 3 случайных элемента и возьмем в качестве опорного элемента медиану выбранной тройки.

Покажем, что среднее время выполнения алгоритма быстрой сортировки $T_{\rm ср}(n) = O(n\log n)$ [Ворожцов, с. 195], [Федоряева, с. 103], [Седжвик, с. 273], [Ахо, с. 242]. Верно следующее рекуррентное соотношение: \(T_{\rm ср}(n) = \frac{1}{n-1}\sum_{k=1}^{n-1} ( T_{\rm ср}(k) + T_{\rm ср}(n-k)) + \Theta(n).\) Это соотношение выписывается из предположения, что все $n-1$ возможных пропорций ($1/(n-1)$, $2/(n-2)$, …, $(n-1)/1$) между размерами двух подмасcивов, на которые разбивается массив из $n$ элементов, равновероятны.

Отсюда \(T_{\rm ср}(n) \leq \frac{2}{n-1}\sum_{k=1}^{n-1}T_{\rm ср}(k) + Cn.\) В [Ахо], [Федоряева] дается доказательство оценки $T_{\rm ср}(n) = O(n\log n)$.

Литература

[Федоряева] Федоряева – Комбинаторные алгоритмы (2011)

[Скиена] Скиена – Алгоритмы. Руководство по разработке (2011)

[КЛРШ] Кормен, Лейзерсон, Ривест, Штайн – Алгоритмы: Построение и анализ (2013)

[Ахо] Ахо, Хопкрофт, Ульман – Структуры данных и алгоритмы (2000) – С. 254-257

[Ворожцов] Ворожцов, Винокуров – Алгоритмы: построение и анализ на Си (2007)

[Седжвик] Седжвик, Уэйн – Алгоритмы на Java (2013)

[ИТМО] Онлайн-курс от Университета ИТМО на платформе Открытое образование