Деревья выражений

АТД “выражение”

Синтаксическое определение АТД “выражение” (в форме Бэкуса-Наура):

<выражение0> ::= число | ( <выражение4> )
<выражение1> ::= <выражение0> | <выражение1> ^ <выражение0>
<выражение2> ::= <выражение1> | - <выражение1>
<выражение3> ::= <выражение2> | <выражение3> * <выражение2> |
     <выражение3> / <выражение2>
<выражение4> ::= <выражение3> | <выражение4> + <выражение3> |
     <выражение4> - <выражение3>

Для целей синтаксического разбора леворекурсивные правила лучше заменить на праворекурсивные [Rossum]:

<выражение0> ::= число | ( <выражение4> )
<выражение1> ::= <выражение0> ^ <выражение1> | <выражение0>
<выражение2> ::= - <выражение1> | <выражение1>
<выражение3> ::= <выражение2> * <выражение3> |
     <выражение2> / <выражение3> | <выражение2>
<выражение4> ::= <выражение3> + <выражение4> |
     <выражение3> - <выражение4> | <выражение3>

АТД “выражение” – это составной тип данных, состоящий из элементов разных типов и ссылок между ними.

Типы данных ($e$ – expression, выражение):

\(e = \mathrm{var}(e_0, e_1, e_2, e_3, e_4),\) \(e_0 = [{\rm Int}], \quad e_1 = [@e, @e, p_1], \quad e_2 = [@e], \quad e_3 = [@e, @e, p_3], \quad e_4 = [@e, @e, p_4].\)

В этом месте следует пояснить используемые нестандартные обозначения. $e, e_i$ – это типы данных. Через $\rm{var}$ обозначена иерархия типов: объект типа $e$ может быть объектов любого из типов $e_i$, $i = 0..4$. Через $[\;]$ обозначена структура (struct). Через $@T$ обозначен тип данных “ссылка на объект типа $T$”, или, короче, “ссылка на тип $T$”. Ссылка на тип $T$ – это объект, указывающий на конкретный объект типа $T$. Через $p_i$ обозначено множество операций, имеющих приоритет, равный $i$:\; $p_1 = {\hat{\;}}$, $p_3 = {*, /}$, $p_4 = {+, -}$.

$\hat{\;}$ – это возведение в степень

Конкретизируем типы: \(e_0 = \{ {\rm num} \in \mathbb N_0 \},\) \(e_1 = \{ {\rm arg}_1, {\rm arg}_2 \in @e, \;\; {\rm op} \in p_1 \},\) \(e_2 = \{ {\rm arg} \in @e \},\) \(e_3 = \{ {\rm arg}_1, {\rm arg}_2 \in @e, \;\; {\rm op} \in p_3 \},\) \(e_4 = \{ {\rm arg}_1, {\rm arg}_2 \in @e, \;\; {\rm op} \in p_4 \}.\) Здесь в фигурных скобках перечислены имена и типы составных частей типов $e_i$. Через $\rm{num}$ обозначено целое неотрицательное число, $\rm{arg}_1, \rm{arg}_2$ – операнды бинарных операций, $\rm{arg}$ – операнд унарного минуса, $\rm{op}$ – операция соответствующего приоритета.

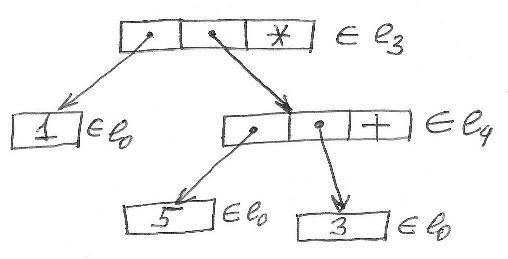
Пример. Выражение 1 * (5 + 3)}. Соответствующая структура данных показана на рисунке. Это структура данных типа “дерево”, точнее, “дерево элементов типа $e$”, обозначение: ${\rm Tree}\langle{e}\rangle$.

Обратная польская запись

Арифметическое выражение можно представить в виде синтаксического дерева. Например, $(2+3) * (4-1)$ представляется так:

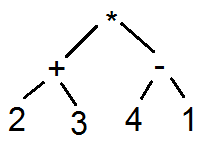
Обратная польская запись выражения получается в результате обратного обхода синтаксического дерева [Ахо, с. 82]. При обратном обходе дерева сначала просматриваются все поддеревья, а потом корень. Другими словами, обходим дерево слева направо, снизу вверх. В данном примере получим строку: $2\ 3\ +\ 4\ 1\ -\ *$.

Обратная польская запись также носит название постфиксной записи выражения.

В обратной польской записи отсутствуют скобки и отсутствует неявный приоритет операций.

Чтобы вычислить результат выражения, нужно просмотреть строку слева направо. Если встречаем операнд, мы помещаем его в стек. Если встречаем знак операции, то мы извлекаем 2 операнда из стека и выполняем над ними вышеуказанную операцию, и результат помещаем в стек. После проведения вычислений в стеке останется результат операции.

Нам понадобится 1 стек, и 1 раз нужно просмотреть выражение слева направо, поэтому вычисление выражения в обратной польской записи эффективно.

СД “дерево выражения”

Варианты реализации:

1) Все узлы дерева одного и того же структурного типа. См. [КерниганРитчи, разд. 6.5, с. 149–153].

Код на ЯП C/C++:

// арифметические операции
enum op_t {
    OP_PLUS, OP_MINUS, OP_MULT, OP_DIV, OP_POW
};

// реализация типа данных "выражение"
struct expr_t {
    int num;
    struct expr_t *arg1, *arg2;
    enum op_t op;
};

// реализация объекта "выражение"
struct expr_t *expr;  // указатель на корень дерева

2) Использование наследования и полиморфизма классов в C++.

Код на ЯП C++:

// тип выражения
enum ExprType {
    EXPR_TYPE_NUM,  // e0
    EXPR_TYPE_POW,  // e1
    EXPR_TYPE_NEG,  // e2
    EXPR_TYPE_MUL_DIV,  // e3
    EXPR_TYPE_SUM_SUB  // e4
};

// операция умножения или деления
enum OpMulDiv {
    OP_MUL, OP_DIV
};

// операция сложения или вычитания
enum OpSumSub {
    OP_SUM, OP_SUB
};

// базовый класс
class Expr {
protected:
    ExprType expr_type;
public:
    virtual ExprType GetExprType() = 0;
};

// число
class ExprNum : public Expr {
public:
    ExprType GetExprType() { return EXPR_TYPE_NUM; }
    int num;
};

// возведение в степень
class ExprPow : public Expr {
public:
    ExprType GetExprType() { return EXPR_TYPE_POW; }
    Expr *arg1, *arg2;
};

// унарный минус
class ExprNeg : public Expr {
public:
    ExprType GetExprType() { return EXPR_TYPE_NEG; }
    Expr *arg;
};

// умножение | деление
class ExprMulDiv : public Expr {
public:
    ExprType GetExprType() { return EXPR_TYPE_MUL_DIV; }
    OpMulDiv op;
    Expr *arg1, *arg2;
};

// сложение | вычитание
class ExprSumSub : public Expr {
public:
    ExprType GetExprType() { return EXPR_TYPE_SUM_SUB; }
    OpSumSub op;
    Expr *arg1, *arg2;
};

Expr *expr;

Литература

[Ахо] Ахо, Хопкрофт, Ульман – Структуры данных и алгоритмы (2000) – С. 82

[Кубенский] Кубенский – Структуры и алгоритмы обработки данных: объектно-ориентированный подход и реализация на C++ (2004) – С. 234

Обратная польская запись

[Rossum] Rossum – Леворекурсивные PEG грамматики

[КерниганРитчи] Керниган, Ритчи – Язык программирования C